体

環のうち, 通常通りに加法と乗法を定めた整数 $\mathbb{Z}$ のように乗法が可換である, すなわち掛け算の順序を $a \cdot b = b \cdot a$ のように入れ替えてもよい環を, 可換環という.

体は可換環であり, かつ乗法について $0$ を除くすべての元に逆元が存在する代数的構造である. 平たく言うなら, $0$ で割ること以外なら自由に足し算, 引き算, 掛け算, 割り算のできる構造のことである.

例

1. 有理数 $\mathbb{Q}$, 実数 $\mathbb{R}$, 複素数 $\mathbb{C}$ の上に通常通りに加法, 乗法を定義した構造は体をなす.
2. 剰余環 $\mathbb{Z}/n\mathbb{Z}$ は乗法について可換なので可換環である. $\mathbb{Z}/n\mathbb{Z}$ は $n$ が素数 $p$ のとき, すなわち $\mathbb{Z}/p\mathbb{Z}$ のとき, $0$ を除くすべての元の乗法に関する逆元が存在し, 体をなす. このことは, ベズーの補題から容易に証明できる.

証明 すべての $0 \lt a \lt p$ であるような $a$ は素数 $p$ と $1$ 以外に公約数を持たず,

$$gcd(a, p) = 1$$

である.

ベズーの補題より, うまく整数 $x, y$ を選ぶことにより,

$$ax + py = 1$$

にできる. すなわち,

$$\begin{align} &\ ax + py = 1 \\\ \Leftrightarrow &\ ax - 1 = - px \\\ \Leftrightarrow &\ ax - 1 \equiv 0 \pmod{p} \\\ \Leftrightarrow &\ ax \equiv 1 \pmod{p} \end{align}$$

となる. このことは, $0$を除くすべての $\mathbb{Z}/p\mathbb{Z}$の元$a$に対して, 乗法に関する逆元 $x$ が存在することを意味している.

よって, $\mathbb{Z}/p\mathbb{Z}$ は体をなす. ■

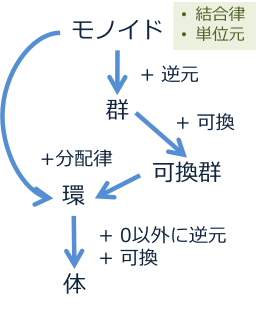
これまでに紹介した代数的構造は、下図の通りにまとめられます。