Diffie-Hellman鍵共有

Diffie-Hellman鍵共有は、前述の通り、一方向性関数をうまく利用することで通信したい二人の間でのみ共通の秘密情報を生成する方法です。

この節を読み始める前に、前提知識として、公開鍵暗号の数学の最大公約数とベズーの補題, 代数的構造 (特に体) , フェルマーの小定理を読んでおくと理解しやすいと思います。

体で説明したとおり、素数$p$によって$\mod{p}$をとって剰余環 $\mathbb{Z}/p\mathbb{Z}$ を構成すると、それは体になります。実は要素数が $p$ のいかなる体も $\mathbb{Z}/p\mathbb{Z}$ と全く同じ構造 (同型といいます) であることが知られていて、この体を $GF(p)$ や $\mathbb{F}_p$ で表します. 前者はGalois Field (ガロア体) の略で、代数学に巨大すぎる業績を残した数学者のガロアの名にちなんでいます。

さて、体は$0$を除いて乗法に関して群をなすのでした。そしてフェルマーの小定理で説明したとおり、群の単位元でない元 $g$ をとって冪乗をとると巡回群 $\langle g\rangle$ をなすのでした。

それでは、Diffie-Hellman鍵共有による秘密情報の共有法をみていきましょう。ここでは通信する二人は、慣習に従ってアリスとボブとします。

1. まずアリスとボブは予め素数 $p$ と 適当な整数 $g$ を生成し、共有しておきます。この情報は盗聴されても構いません。
2. アリスは自由に整数 $a$ をひとつ生成して、$GF(p)$上で $g^a$ を計算します (慣れないうちは、$\mathbb{Z}$上で$g^a \pmod{p}$ を計算すると言い換えてもいいです。ただし、あんまり$\mod{}$に引きずられすぎると、楕円曲線暗号などとの対応が見えづらくなると思います)
3. ボブも同じように整数 $b$ を生成して$GF(p)$上で$g^b$を計算します
4. アリスはボブに$g^a$を送信し、ボブはアリスに$g^b$を送信します。これらの情報は盗聴されても構いません。
5. アリスは受信した$g^b$と、自分しか知らない整数である $a$ をつかって、$(g^b)^a = g^{ab}$ を計算します
6. ボブも同様にして、$(g^a)^b=g^{ab}$を計算します

こうして、アリスとボブは共通する情報 $g^{ab}$ を生成することができました。

なお、1で"任意"ではなく "適当な整数 $g$" としているのは、生成する $g$ によっては離散対数問題を解くのがそれほど難しくない場合があり、実は生成する $g$ に関して制約があるからです。

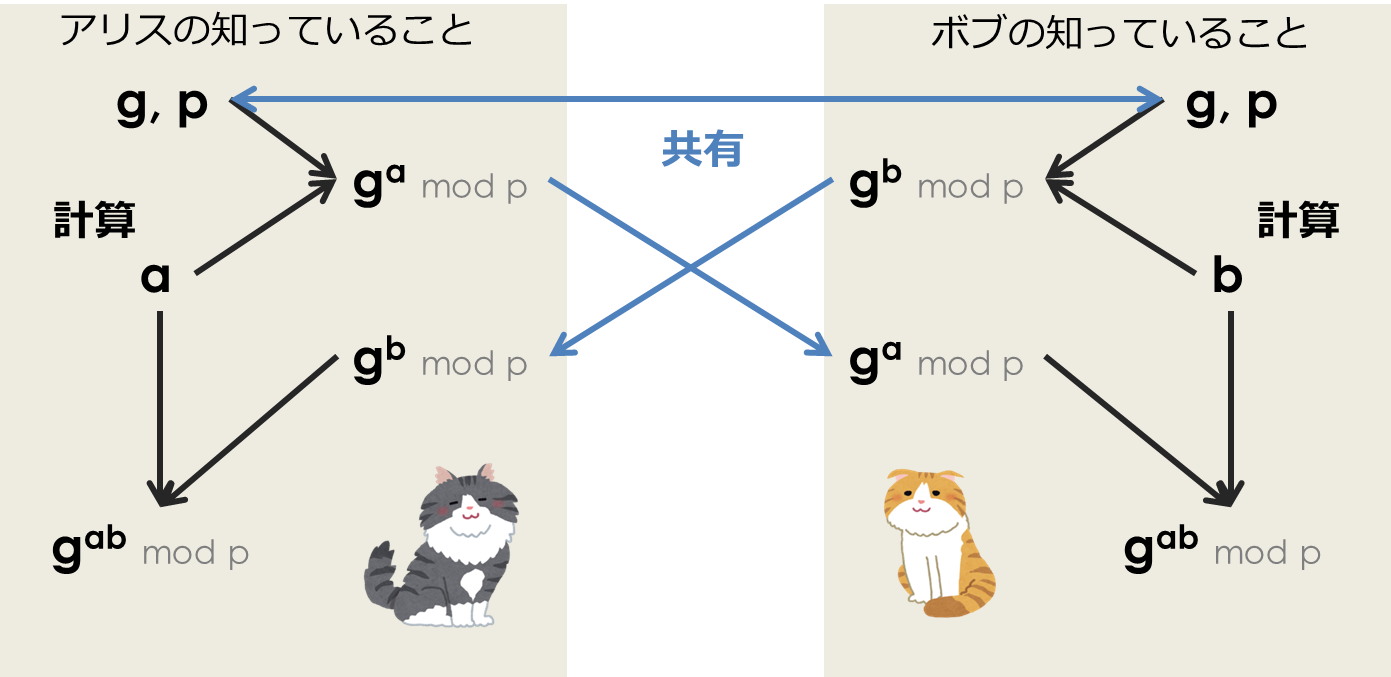
さて、この手順において $g, p, g^a, g^b$はアリス・ボブ間で共有するために伝送路上を流れます。この情報は盗聴されても構わないのでした。これは、ある仮定の上に、これらの情報を盗聴されたとしても、盗聴者が$g^{ab}$を計算することが困難であるからです。

盗聴者がアリスと同じように $g^{ab}$ を作り出すには、アリスしか知らない整数 $a$ を、 $f: g^a \pmod{p} \rightarrow a$ という逆方向の計算方法 $f$ をみつけて求めなければなりません。ボブと同じように$b$から$g^{ab}$を計算する場合も、やはり$g^b \rightarrow b$という逆算が必要です。

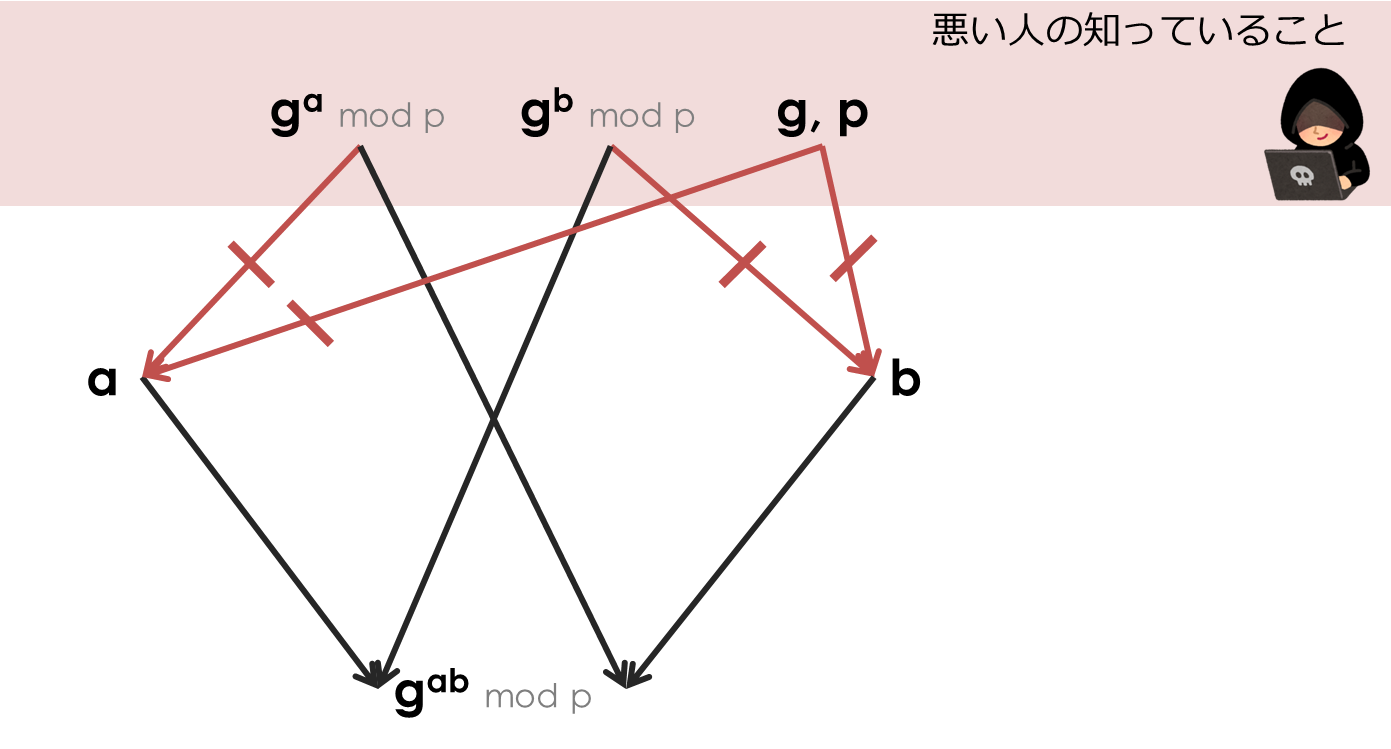
この逆向きの計算を解くことを離散対数問題 (DLP: Discrete Logarithm Problem) といい、いまのところ容易に解く方法、すなわち多項式時間アルゴリズムが発見されておらず、困難であると考えられています。もしも、離散対数問題を簡単に解くアルゴリズムが見つかってしまうと、伝送路を流れる情報から盗聴者も秘密情報を生成できてしまうため、Diffie-Hellman鍵共有は安全でありませんが、今のところ離散対数問題は困難と考えられているわけです。

なお、離散対数問題というのは、一般にどのような群の元から生成される巡回群についても考えることができます。すなわち、群 $G$ の元 $g \in G$ から生成される $\langle g \rangle$ について、$a \in \langle g \rangle$ と $a^x$ から $x$ を計算するのが困難であるというのが離散対数問題です。

実は離散対数問題は、巡回群を生成するもととなる群によっては、暗号の用に供することができるほど困難にならないことがわかっていて、標準化されて暗号に使われているのは今のところ次の2つです。ひとつは前述の$GF(p)$の乗法に関する群の元から生成される巡回群を使うもので, Diffie-Hellman鍵共有やElGamal暗号はこれを利用します。もうひとつは、楕円曲線上の有理点のなす群の点から生成した巡回群を利用するもので、楕円曲線Diffie-Hellman鍵共有 (ECDH) や楕円曲線暗号で実際に使用されています。他にも超楕円曲線の上のヤコビ多様体から生成する場合にも暗号用に使えることがわかっていますが、いまのところSSL/TLSなどでは使われていないようです。

閑話休題

上で "離散対数問題を簡単に解くアルゴリズムが見つかってしまうと、伝送路を流れる情報から盗聴者も秘密情報を生成できてしまうため、Diffie-Hellman鍵共有は安全で"ないと述べましたが、その逆と論理的に同値 (裏) な "離散対数問題を簡単に解けなければ、Diffie-Hellman鍵共有は安全である" は正しいといえるでしょうか。

実はこれは言えません。なぜならば、離散対数問題が困難であったとしても、$g, p, g^a, g^b$ から、$g^a \rightarrow a$ や $g^b \rightarrow b$ という逆算を経ずに直接$f(g, p, g^a, g^b) \rightarrow g^{ab}$ と計算してしまうような $f$ を見つけられる可能性までは否定できないからです。この "$g, p, g^a, g^b$ から $g^{ab}$ を計算する" 問題をDiffie-Hellman問題 (DHP: Diffie-Hellman Problem) といいます。また、この問題を解くのが困難であるという仮定をCDH (Computational Diffie-Hellman) 仮定

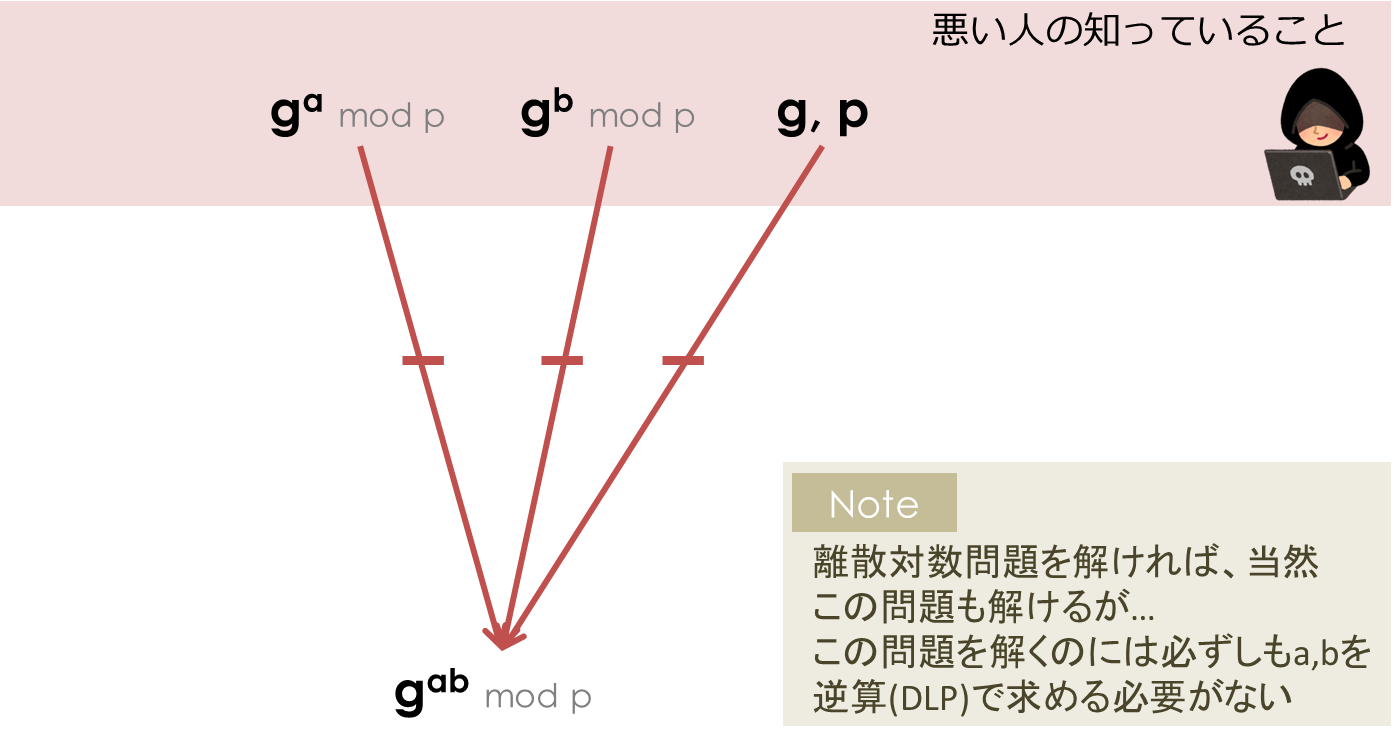
明らかに、離散対数問題が解ければこの問題も解けるため、問題の困難性しては $DLP \ge DHP$ という関係になっています。問題を解くのが困難であるという仮定については、$DHP$の方がより強い仮定をおいていることになります。