公開鍵暗号ってなんだっけ

公開鍵暗号は鍵生成、暗号化、復号のアルゴリズムの組として表されます。

公開鍵暗号の鍵生成アルゴリズムは、誰にも公開しない秘密鍵$sk$と、通信したいすべての人に公開する公開鍵$pk$を生成します ($sk \ne pk$とする。) 暗号化アルゴリズム$Enc$は公開鍵$pk$を使って、平文$m$から暗号文$c :=Enc(pk, m)$を作ります。復号アルゴリズム$Dec$は秘密鍵$sk$を使って、暗号文$c$から平文$m := Dec(sk, c)$を復号します。

このように、暗号化の際に使用する鍵$pk$と復号に使用する鍵$sk$が異なるため、非対称暗号 (asymmetric cipher) とよばれることもあります。

暗号化に使用する鍵 $pk$ は公開情報であって、暗号化アルゴリズム $Enc$ も公開情報ですので、公開鍵暗号の安全性を考える場合には、攻撃者は選択平文攻撃 (CPA) 以上の攻撃が可能であることを常に想定しなければなりません。すなわち、暗号の用に供するためには、少なくとも IND-CPA (選択平文攻撃での識別不可能性) を証明できる必要があります。

ElGamal暗号

ElGamal暗号は、公開鍵暗号の一方式であり、$GF(p)$の $0$ を除いて乗法に関してなす群の要素から生成される巡回群を利用します。具体的には次のような方式です。

1. Diffie-Hellman鍵共有と同様に、まずは、素数$p$と適当な $g \in (\mathbb{Z}/p\mathbb{Z})^{\times}$ を生成して公開しておきます
2. 次に鍵生成を行います。整数 $x$ をランダムに選び、 $g^x$ を生成します。$x$ を秘密鍵、$g^x$ を公開鍵とし、 $g^x$ は公開します
3. 公開鍵 $g^x$ をもつ人は、乱数$r$ を生成して $g^r$ を計算してから、平文$m$ に対して $(g^r, mg^{xr})$ というペアを計算し、これを暗号文とします
4. 秘密鍵 $x$ をもつ人は、暗号文 $(g^r, mg^{xy})$ を受け取ったのちに、$(g^r)^x = g^{xr}$ を計算し、この$g^{xy}$ で $mg^{xy}$ を割ります。すると、$\frac{mg^{xy}}{g^{xy}}=m$ となり、復号することができます

もしも$g, p, g^x$から$x$を逆算できた場合には、これらは公開情報でしたから、盗聴者を含め誰でも秘密鍵を計算で求めることができ、よって暗号化のみならず復号まで自由にできてしまいます。言い換えると、もしも離散対数問題が解けるならば、秘密鍵を復元する (こういった攻撃を、鍵復元攻撃 (key recovery attack) という) ことが可能となって、ElGamal暗号は安全ではなくなります。

ElGamal暗号の安全性

共通鍵暗号の章で既に説明していますが、暗号文から平文に関するいかなる部分情報も漏れない (情報を少しでも得られるような確率多項式時間アルゴリズムを構成することができない) 安全性を強秘匿性 (SS: Semantic Security) といいます。

また、攻撃者が選んだ2つの平文 $m_1, m_2$ のうちどちらか一方だけを暗号化して攻撃者に返すようなアルゴリズムがあり、攻撃者がそのアルゴリズムを利用可能と仮定したときに、 $m_1, m_2$ のいずれが暗号化されたのか $\frac{1}{2} + negligble$ の確率でしか言い当てられないとき、すなわち「当てずっぽう」が攻撃者にとって最良の戦略であるとき、この安全性を識別不能性 (IND: Indistinguishability) というのでした。

そして、INDとSSは等価であることが証明されているのでした。INDの方が証明に使いやすく、SSの方が意味するところを理解しやすいため、証明にはINDをつかって「いかなる平文の部分情報も漏れない」と解釈することがよくあります。

ここで、$negligible$ は無視可能関数 (negligible function) を表しています。関数$f$が無視可能関数であるとは、どんな正の定数 $c$ をとってきても、パラメーター $k$ を十分大きくとれば $\frac{1}{k^c}$ よりも小さくできるような関数のことです。すなわち十分 $k$ を大きくとることで、 $f(k) \lt \frac{1}{k^c}$ とできるとき、$f$を無視可能関数といいます。なんとなく $\varepsilon{}-\delta$論法に似ていると感じた方もおられると思いますが、実際このことはどんなに小さな数 $\frac{1}{k^c}$ に対しても $k$ を十分大きくとれば、その小さな数未満におさえられることを意味しており、 $\varepsilon{}-\delta$と同じで 漸近的に$0$になる といえます。そのため 無視可能 なのです。パラメーター $k$ のことをセキュリティパラメーターといって、鍵長やブロック長がセキュリティパラメーターになります。

攻撃者の能力としては、公開鍵暗号では CPA (選択平文攻撃), CCA (選択暗号文攻撃), CCA2 (適応的選択暗号文攻撃) が考えられ、これらの条件のもとでINDであることを、それぞれIND-CPA, IND-CCA, IND-CCA2 といいます。

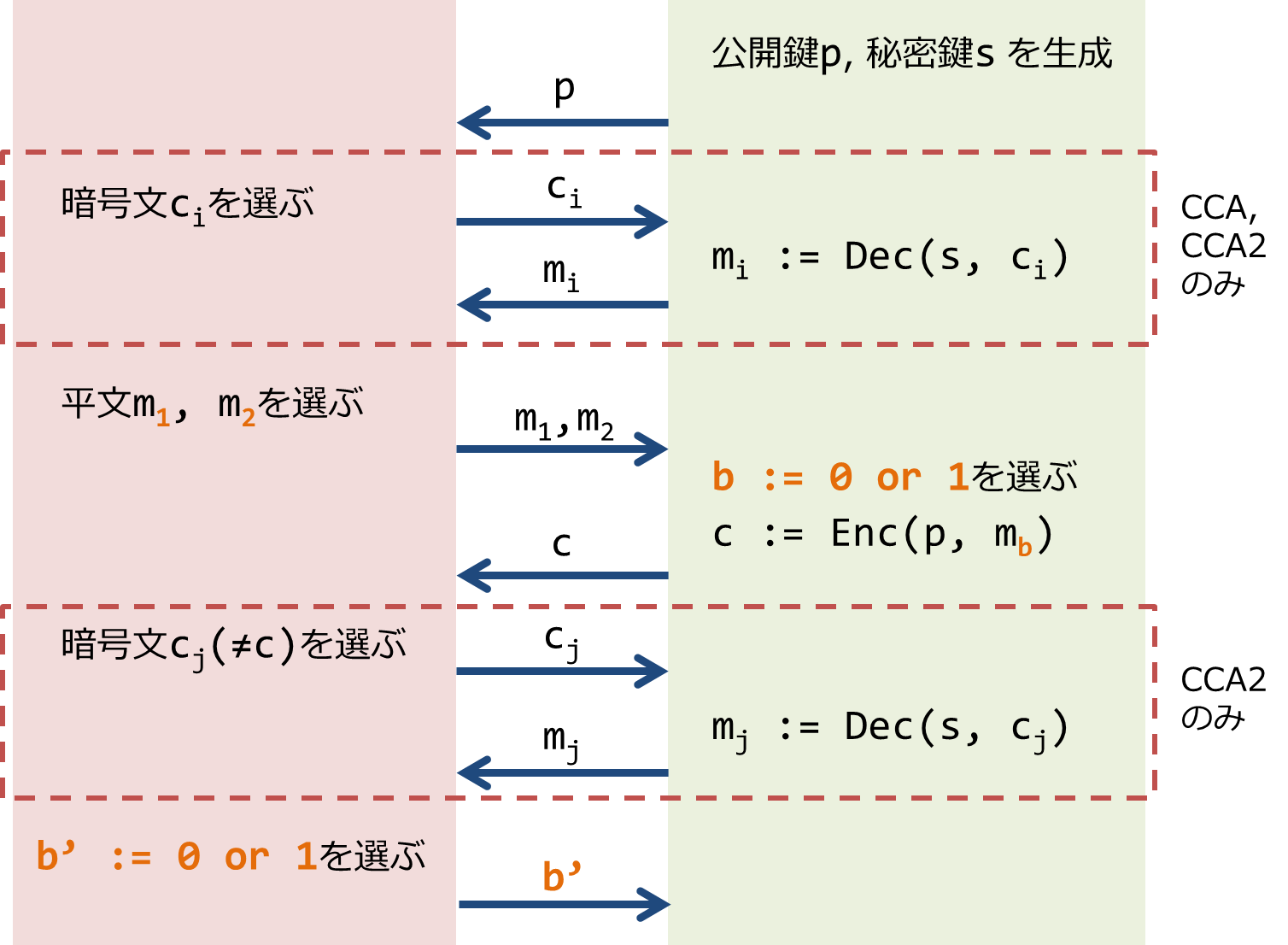
IND-attack ($attack \in \{CPA, CCA, CCA2\}$) は下図のゲームにおいて、$\frac{1}{2} + negligible$ の確率でしか $b^{\prime} = b$ とならない安全性です。左側の赤い四角形で覆われた領域が攻撃者の行動で、右側は攻撃者ではなく挑戦者と呼ばれ、これは攻撃者に利用できる攻撃者以外の機能のあつまりです。

INDも後述するNMも、このような攻撃者と挑戦者のゲームにおいて、攻撃者が勝利する確率が高い (優位性が高い) 場合には安全でなく、優位性が十分に低ければ安全と考えます。

さて、それではElGamal暗号はこのIND-CPA, IND-CCA, IND-CCA2 の意味の安全性を満たすでしょうか。

まず、攻撃者は公開情報として $g, p, g^x$ を手に入れます。つづいて、平文をふたつ $m_1, m_2$ を選び、２つのうちどちらかを確率的に暗号化するアルゴリズムに入力して出力 $(c_1, c_2)$ を得ます。$(c_1, c_2)$は$m_1$を暗号化した結果である $(g^r, m_1g^{xr})$ か $(g^r, m_2g^{xr})$ のいずれかです。よって、$c_2/m_1$ か $c_2/m_2$ のいずれかは、$g^{xr}$ となります。どちらで割った結果が$g^{xr}$であるか判定できる場合は、すなわち暗号化したのが$m_1$か$m_2$かを識別できるということを意味するので、この場合はCPAでの識別不可能性 (IND-CPA) を満たしません。

今のところ、$g, g^r, g^x$ を所与として、$g^{xr}$ かランダムに選んだ$c$に対する$g^{c}$ かのいずれかを受け取ったときに、それが$g^{xr}$ であるか否かを言い当てることは困難であると考えられていて、この困難性を仮定すると、IND-CPAを満たすといえます。この問題をDDH問題 (Decisional Diffie-Hellman Problem) といい、それが困難であるという仮定をDDH仮定といいます。ElGamal暗号は DDH仮定の上でIND-CPA といいます。

ElGamal暗号は IND-CPA ではありますが、IND-CCA, IND-CCA2 の意味では安全な暗号ではありません。ただし、ElGamal暗号をベースとして構成したCramer-Shoup暗号はIND-CCA2となることが証明されています。

ElGamal暗号と頑強性

復号はできないものの、観測した暗号文と何らかの関連をもつ別の暗号文を作れる場合、たとえば送金額を暗号化して指定する場合に「かける1000」した暗号文を作成して差し替えることができるとなにかと問題がありそうです。

このようなことができないとき、その安全性を頑強性 (NM: Non-Malleability) といいます。

ElGamal暗号は以下のように元の暗号文に対応する平文と関連をもつ別の平文の暗号文を作れてしまうため、NMの意味では安全ではありません。

1. 攻撃者が暗号文 $(g^r, mg^{xr})$ を傍受する
2. 攻撃者は任意に整数$k$を選んで、次のような暗号文をつくる $(g^r, kmg^{xr})$

この暗号文を受信者が復号すると、$\frac{kmg^{xr}}{(g^r)^x}=\frac{kmg^{xr}}{g^{xr}}=km$ となるため、上の手順によって、攻撃者は元の暗号文に対応付く平文$m$を$k$倍した値$km$の暗号文を作成できたことになります。